A Transient Thermal Model
When a transient thermal analysis with non-physical temperature results is generated in Ansys (Biot number), whether via the APDL interface or Mechanical (Workbench), there are several ways to standardize the data sets. An example is a temperature result that is outside any temperature applied to a model. This may be seen with extreme Biot numbers (high convection coefficients) or with inappropriate time substep sizes, and is more common with high-order thermal elements.
This article shows an example of this difficulty, and gives suggestions on reducing its occurrence.
Example | Thermal Analysis with Known Convection Load & Convection Coefficient
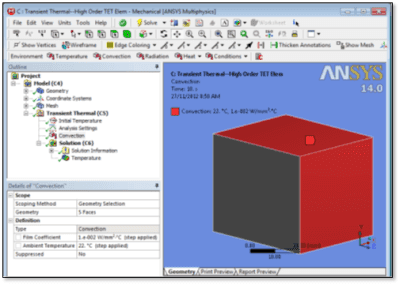
In a test model, a rectangular block with an initial temperature of 300C has had a convection load of a fluid at 22C and a convection coefficient of 0.01 W/mm2 /C applied to five of its six faces:
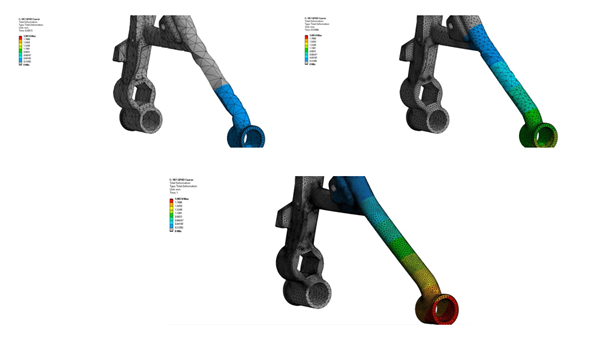
After a short substep, temperatures that are greater than 300C are seen… this is not a physically realistic response:
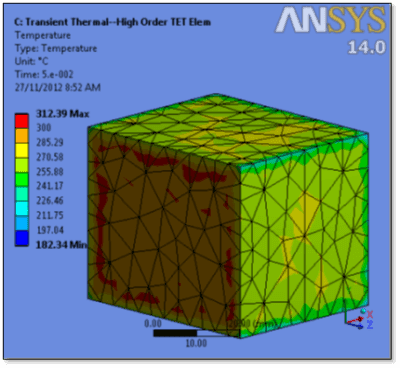
The above temperature result is affected by the use of high-order elements, tetrahedral shapes, and high Biot numbers. Means of reducing the problem include smaller elements, low-order elements, and hex meshing.
Biot Numbers and Model Meshing in Ansys Mechanical
The same model meshed with hex element of the same general size produces a not quite perfect, but much better result at the same substep:
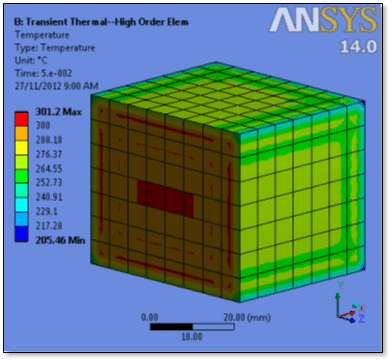
Temperatures just slightly above 300C are seen. The non-physical temperatures are not seen if low-order elements are employed:
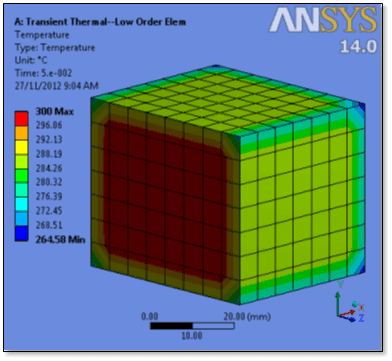
Thermal results are often moved into structural models. In Ansys Workbench, the same geometry can have a different mesh applied, and the temperatures can be mapped from the thermal to the structural system.
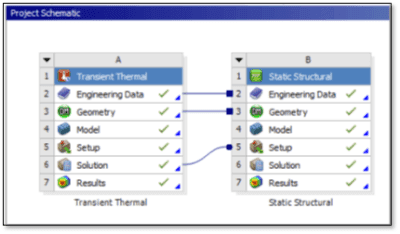
Transient Thermal Analysis | Low-Order Hex
A thermal system can use a mesh of low-order hex and tet elements in order to avoid non-physical results, while the associated structural system can mesh the same geometry with high-order elements in order to give good structural results, particularly with tet elements. The mapping includes controls for the imported body temperature in the structural system:
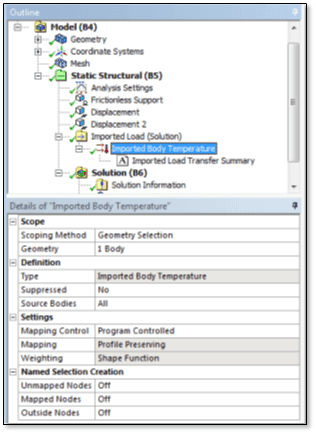
Conclusions | Managing Non-Physical Temperature Results in a Transient Thermal Analysis
In thermal FEA models, choices of elements size, shape and order, as well as high Biot number convective loads, can sometimes result in non-physical temperature results such as temperatures that are higher or lower than any applied temperature. In transient models, the use of small time substeps can amplify the effect with high-order elements.
Fewer problems of this sort are seen in thermal models that use low-order elements such as 4-node tet elements and 8-node brick elements. Related structural FEA models of the same geometry can use high-order structural elements, and recent versions of Ansys Mechanical Workbench, such as v14.0, can map temperatures between the non-matching meshes. There are a number of user-set controls for how the mapping is performed.
For CFD/Thermal Management Consulting services, find out more HERE.
Difficulties in thermal responses will still be occasionally seen with low-order thermal elements. The use of layers of elements that are thin at exterior surfaces can be used in attempts to address this (reducing the Biot number) in transient thermal. The difficulty may also sometimes be seen in thermal elements that have different convective or convection loads on two faces of one element. Work-around methods could include small elements on edges, or a small strip on one side of an edge with no convective load applied.
The Ansys Mechanical APDL interface has mapping methods for each convection loads and temperatures using the BFINT command. The mapping methods available in the most recent Workbench Mechanical interface are more advanced, and offer higher success rates for mapping between non-matching meshes. In this way, many non-physical thermal response difficulties can be avoided, while still performing related structural analyses with high-order elements.
Additional Ansys Software Tips & Tricks Resources
- For guidance on Pre-Stressed Modal Analysis Linked to Nonlinear Static Analysis
- For support on Compiling and Loading User Defined Functions (UDFs)
- For Extreme Thermal Expansion Modeling in Mechanical
- For enhancing Autonomous Vehicle Hazard Recognition
- For advanced Analysis of Models Exhibiting Cyclic Symmetry
- Deploying *TREAD in Mechanical APDL to Read External Data
- For Replicating Base Acceleration in Harmonic Analysis
- Setting up Automatic Messages in Ansys Mechanical
- For Constructing Element Quality Plots in Mechanical WB
- For APDL Command Function Post-Response Spectrum Analysis